2016 ARTEMIS SCIENCE NUGGETS
Experimental whistler wave dispersion relation in the solar wind
by David Stansby
Imperial College London
Introduction
Along with a ubiquitous broadband spectrum of turbulence, the electromagnetic fields in the solar wind occasionally show evidence of larger amplitude coherent waves. Full characterisation of these waves requires independent measurement of their frequency and wavevector. We have achieved this for whistler waves in the solar wind by exploiting high frequency (128 samples /s) electric and magnetic field measurements on board the two ARTEMIS spacecraft.
|
| Figure 1. A cartoon of the ARTEMIS and LADEE orbits around the Moon [not to scale]. LADEE’s science orbit ranged between 50-250 km altitude while the ARTEMIS probes are much more eccentric and travel farther from the Moon. |
Observations
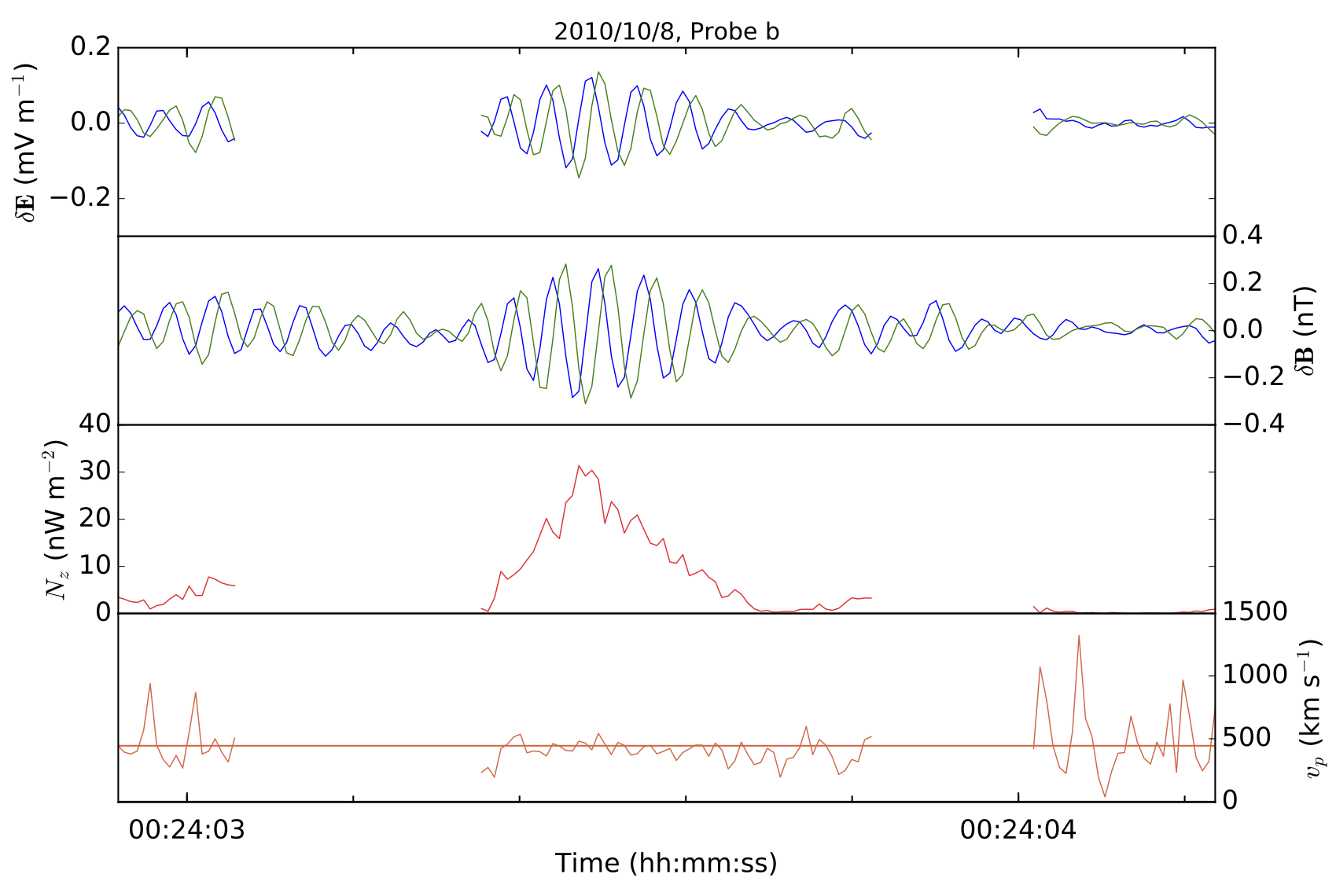
Figure 1 shows the electric (top panel) and magnetic (2nd panel) fields for a single whistler wave. These two measurements allow calculation of the Poynting flux (3rd panel) and phase speed (4th panel). Along with a measurement of the wave frequency in the spacecraft frame, this allowed us to determine the spacecraft frame frequency and wave vector without assuming a dispersion relation or using Taylor’s hypothesis. The direction of the Poynting flux along with minimum variance analysis of the circularly polarised waveform revealed the direction in which the wave was propagating.
Results
The wave properties were calculated for 289 individual waves across seven different 10 minute intervals. 98% of the waves travelled anti-sunward, and all travelled within 20 degrees of the background magnetic field. This is exactly what we expect if the whistlers were generated by the electron heat flux instability. Because they travelled anti-sunward, they could not resonantly interact with the electron strahl.
|
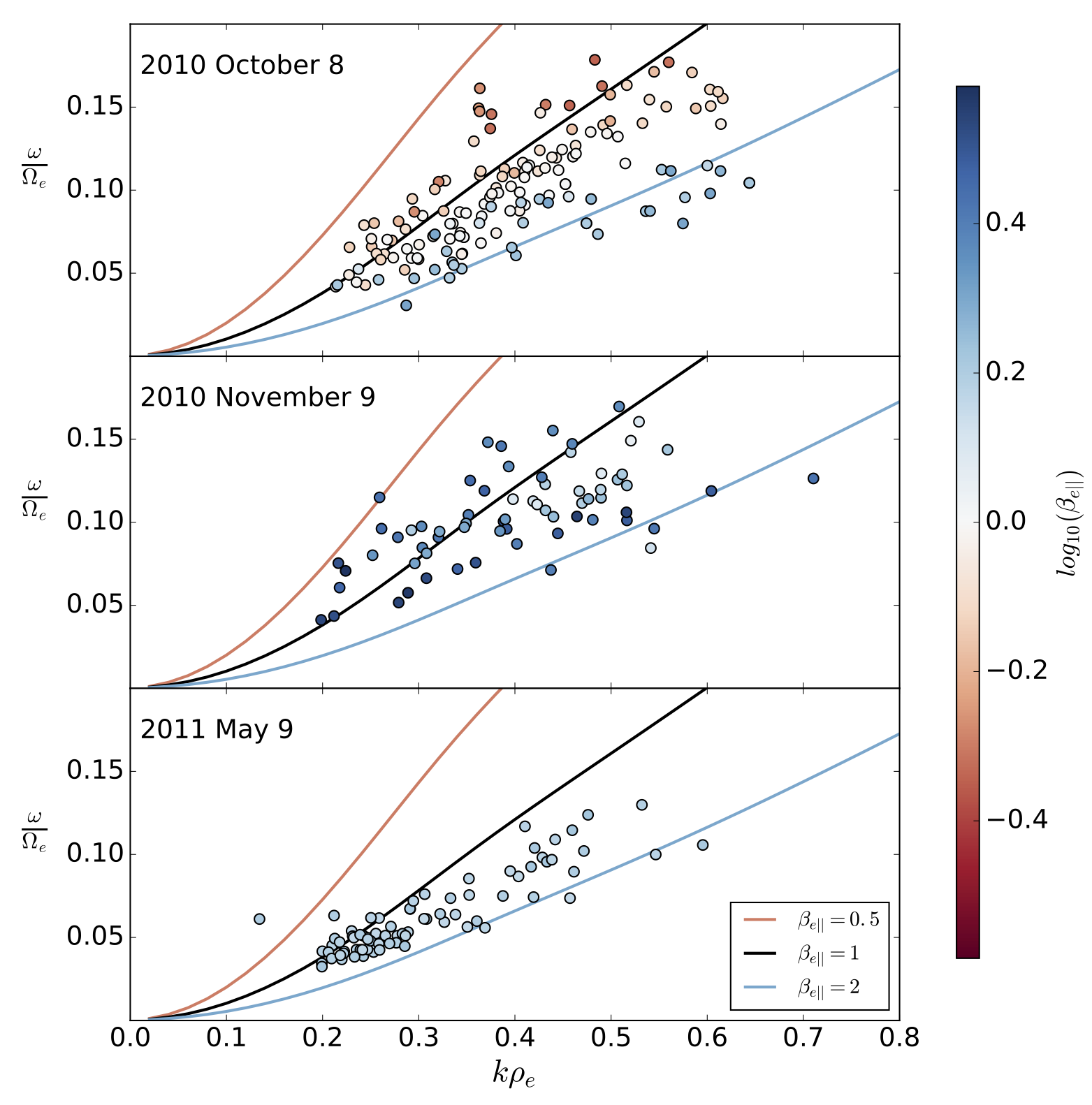
| Figure 2. Experimental dispersion relation with points coloured by the local parallel electron beta. Different panels correspond to different dates of observation, and over plotted lines are theoretical dispersion relations for different beta values. |
Figure 2 shows the experimental frequency-wavevector measurements for the different days of measurement, along with whistler wave dispersion relations for different parallel beta values. The experimental dispersion relation agrees well with the linear predictions in the top and bottom panels, with the large range of electron beta explaining the spread in the data. The middle panel does not appear to agree with linear theory - this may be because strong drifting populations on this day are not taken into account in the dispersion solver we used.
Conclusion
We have constructed an experimental dispersion relation for large amplitude whistler waves in the solar wind for the first time to show that:
- Their dispersion is strongly affected by the local electron parallel beta
- Their generation method is most likely the electron heat flux instability
- They cannot be responsible for resonantly scattering strahl electrons
References
Stansby, D., Horbury, T. S., Chen, C. H. K., & Matteini, L. (2016). EXPERIMENTAL DETERMINATION OF WHISTLER WAVE DISPERSION RELATION IN THE SOLAR WIND. The Astrophysical Journal, 829(1), L16. doi:10.3847/2041-8205/829/1/L16Biographical Note
David Stansby is a PhD student at Imperial College London. For more information see https://www.imperial.ac.uk/people/david.stansby14
Please send comments/suggestions to
Emmanuel Masongsong / emasongsong @ igpp.ucla.edu